广州数学大讲坛第七期
第六十六讲——北京师范大学张阳阳博士后学术报告
题目：分数次球Banach Sobolev空间的端点理论
时间：2024年10月16日（星期三）下午14:00——15:00
地点：腾讯会议（会议ID：340-538-087，密码：241016）
报告人：张阳阳
摘要：函数空间实变理论特别是(Gagliardo型分数次)Sobolev空间理论在数学和物理等相关领域中起着重要的作用. 对任意s∈(0,1)和p∈(1,∞), Gagliardo型分数次Sobolev空间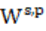
(
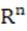)定义为全体满足以下半范有限的可测函数组成的集合
然而, (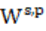
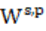)在端点s=1处无法回到经典的Sobolev空间, 这是()一个众所周知的缺陷. Bourgain, Brézis和Mironescu在[Optimal Control Partial Diff. Eq. 2001]证明了在有界区域Ω上(1-s)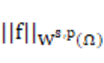
在s趋近于1时可以回到经典Sobolev半范
, 此即著名的BBM公式, 也见[J. Anal. Math., 2002]. Brézis等人[Russian Math. Surveys 2002]将BBM公式推广到n维欧氏空间中, 也见[JFA 2019]. Brézis, Van Schaftingen和Yung于[PNAS, 2021]通过将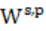
(
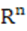)半范中的强型Lebesgue范数替换成弱型Lebesgue范数完美的弥补了
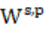()空间临界情形的缺陷, 得到了经典Sobolev空间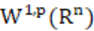
新的等价刻画, 并利用该公式给出了临界情形下的分数次Sobolev和Gagliardo—Nirenberg不等式. 该报告主要讲解基于球Banach函数空间X的分数次Sobolev空间及其上的端点理论, 以及非平移不变情形与平移不变情形的证明区别。
报告人简介：
张阳阳，北京师范大学数学科学学院博士后，主要从事调和分析函数空间及其应用的研究，已在Math. Ann.，Adv. Math.，J. Funct. Anal.和J. Geom. Anal.等杂志发表论文多篇。
