近日，我院博士生曾志城与导师王晓峰教授、湖州师范学院教授胡璋剑合作，完成了Fock型空间上Hankel算子的有界性、紧性及Schatten类的研究，相关结果发表在数学类顶级刊物Transactions of the American Mathematical Society。
01 研究背景
Hankel算子来源于Hankel矩阵，是数学中非常重要的一类算子，在数字信号处理、数值计算、系统控制等领域均有广泛的应用，与复分析、函数论、调和分析及算子理论等数学分支有密切联系。Hankel算子的有界性、紧性和Schatten类性质是这类算子最基本与最重要的性质。Fock空间是高维复空间
上的全纯函数空间，是很重要的一类函数空间，在量子力学等中有重要的应用。Fock型空间是一大类加权Fock空间(包含了经典Fock空间)，这类空间的再生核点估计与Bergman度量和经典Fock空间情况有很大差别，经典方法不再适用，结构非常复杂，研究其上的Hankel算子的有界性、紧性和Schatten类性质是充满挑战性的问题。
02 研究内容
在论文中作者研究了Fock型空间上以局部可积函数为符号的Hankel算子的有界性、紧性和Schatten类性质。证明的关键步骤是通过研究Bergman度量的各向异性构造一类辅助函数，用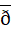
-技巧得到Fock型空间中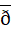-方程解的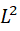
估计，以及用纯粹分析的技巧得到精确的再生核积分估计；然后用BDA函数（bounded distance to analytic functions）刻画了Hankel算子的有界性，用VDA函数（vanishing distance to analytic functions）刻画了Hankel算子的紧性，用IDA函数（integrable distance to analytic functions）刻画了Hankel算子的Schatten类。还得到了Toeplitz算子Schatten类性质的完整刻画。
03 研究相关
Transactions of the American Mathematical Society创刊于1900年，是由美国数学学会主办的综合性数学刊物，年收录论文200余篇，是公认的数学类顶级期刊，具有很高的学术声誉。该研究得到了国家自然科学基金及广州大学研究生“基础创新”项目的支持，作者曾志城是我院在读博士研究生，其本科和硕士阶段的学习也是在我院完成的。
学院高度重视研究生培养质量的提升，近年来出台了一系列的政策支持和鼓励研究生开展高水平学术研究，定期举行青年数学学术论坛，为研究生创设良好的学术发展平台。近年来研究生在Trans. AMS、Math. Z.、JDE、Z. Angew. Math. Phy.、J. Math. Boilogy、DCDS、IEEE Transactions系列、数学教育学报等国际国内一流杂志上发表了多篇高水平论文，培养了首届世界华人数学家联盟年会最佳论文奖获得者清华大学左怀青教授、国家特支计划教学名师张蜀青教授等一批杰出毕业生。该研究成果的取得也是学院研究生教育培养质量不断提升的重要标志。
论文链接
https://www.ams.org/journals/tran/0000-000-00/S0002-9947-2024-09290-5/
